BJT电路的负载线分析

到目前为止，我们一直在研究基于β水平的BJT分析操作点(Q-point)．在这个讨论中，我们将检查一个给定的电路条件如何有助于确定可能的工作点或q点的范围，并建立实际的q点。

什么是载重线分析

在任何电子系统中，施加在半导体器件上的负载通常会对器件的操作点或操作区域产生重大影响。

如果通过图形图进行分析，我们可以画出穿过装置特性的直线来确定所施加的载荷。负荷线与设备特性的交点可用于确定运行点或设备的q点。由于明显的原因，这种分析被称为负荷线分析。

如何实施载重线分析

图4.11(a)所示的电路确定了一个输出方程，该方程提供了变量IC和VCE之间的关系，如下所示:

Vce = VCC - icrc (4.12)

另外，如图(b)所示的晶体管输出特性也提供了两个变量IC和VCE之间的关系。

这基本上帮助我们得到一个基于方程的电路图和一系列特征，通过图形表示与类似的变量。

当它们定义的约束同时得到满足时，它们的共同结果就建立起来了。

或者，这可以理解为从两个并行方程中得到的解决方案，其中一个是在电路图的帮助下建立的，而另一个是来自BJT数据表特征。

在图4.11b中，我们可以看到BJT的特征IC vs VCE，所以现在我们可以在特征上叠加一条由Eq(4.12)描述的直线。

在特征上跟踪Eq(4.12)最简单的方法可以通过以下规则执行:任何直线都是由两个不同的点决定的。

通过选择IC = 0mA，我们发现横轴成为其中一个点所在的直线。

也通过在Eq(4.12)中替换IC = 0mA，我们得到:

这决定了直线的一个点，如下图4.12所示:

如果我们让VCE = 0V，那么垂直轴就是第二点所在的直线。在这种情况下，现在我们可以发现IC可以用下面的方程来评估。

从图4.12可以清楚地看出。

通过连接由等式确定的两点。(4.13)和(4.14)可以画出Eq 4.12所建立的直线。

图4.12所示的这条线被认为是载重线因为它的特征是负载电阻RC。

通过求解IB的建立水平，可以固定实际的q点，如图4.12所示

如果我们通过改变RB值来改变IB的大小，我们发现q点沿负载线向上或向下移动，如图4.13所示。

如果我们保持一个恒定的VCC，而只改变RC的值，我们发现载荷线的位移如图4.14所示。

如果我们保持IB不变，我们发现q点改变了它的位置，如图4.14所示。如果我们保持RC不变，只改变VCC，我们看到载重线移动如图4.15所示

求解一个实际载重线分析实例

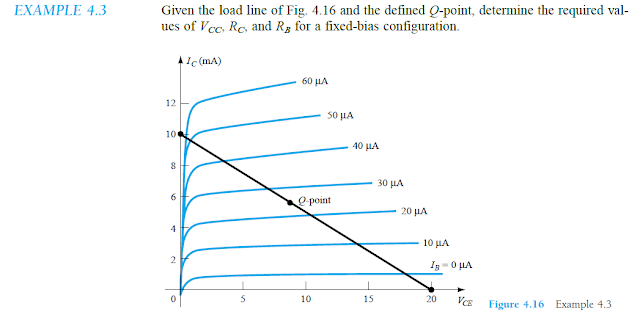
参考:https://en.wikipedia.org/wiki/Load_line_(电子)